![[C# Helper]](../banner260x75.png)
|
|
 |
![[Beginning Database Design Solutions, Second Edition]](db2_79x100.png)

Title: Find a polynomial least squares fit for a set of points in C#
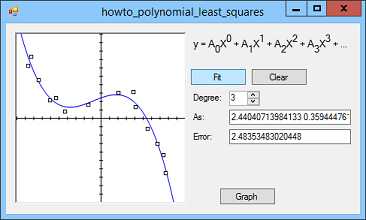
This example shows how to make a polynomial least squares fit to a set of data points. It's kind of confusing, but you can get through it if you take it one step at a time. The example Find a linear least squares fit for a set of points in C# explains how to find a line that best fits a set of data points. If you haven't read that example yet, you should do so now because this example follows the same basic strategy. With a degree d polynomial least squares fit, you need to find the coefficients A0, A1, ... Ad to make the following equation fit the data points as closely as possible:
A0 * x0 + A1 * x1 + A2 * x2 + ... + + Ad * xd The goal is to minimize the sum of the squares of the vertical distances between the curve and the points. Keep in mind that you know all of the points so, for given coefficients, you can easily loop through all of the points and calculate the error. If you store the coefficients in a List<double>, then the following function calculates the value of the function F(x) at the point x.
// The function. public static double F(List<double> coeffs, double x) { double total = 0; double x_factor = 1; for (int i = 0; i < coeffs.Count; i++) { total += x_factor * coeffs[i]; x_factor *= x; } return total; } The following function uses the function F to calculate the total error squared between the data points and the polynomial curve.
// Return the error squared. public static double ErrorSquared(List<PointF> points, List<double> coeffs) { double total = 0; foreach (PointF pt in points) { double dy = pt.Y - F(coeffs, pt.X); total += dy * dy; } return total; } The following equation shows the error function:
To simplify this, let Ei be the error in the ith term so:
The steps for finding the best solution are the same as those for finding the best linear least squares solution:
As was the case in the previous example, this may sound like an intimidating problem. Fortunately the partial derivatives of the error function are simpler than you might think because that function only involves simple powers of the As. For example, the partial derivative with respect to Ak is:
The partial derivative of Ei with respect to Ak contains lots of terms involving powers of xi and different As, but with respect to Ak all of those are constants except the single term Ak * xik. All of the other terms drop out leaving:
If you substitute the value of Ei, multiply the -xik term through, and add the As separately you get:
As usual, this looks pretty messy, but if you look closely you'll see that most of the terms are values that you can calculate using the xi and yi values. For example, the first term is simply the sum of the products of the yi values and the xi values raised to the kth power. The next term is A0 times the sum of the xi values raised to the kth power. Because the yi and xi values are all known, this equation is the same as the following for a particular set of constants S:
This is a relatively simple equation with d + 1 unknowns A0, A1, ..., Ad. When you take the partial derivatives for the other values of k as k varies from 0 to d, you get d + 1 equations with d + 1 unknowns, and you can solve for the unknowns. Linear least squares is a specific case where d = 1 and it's easy to solve the equations. For the more general case, you need to use a more general method such as Gaussian elimination. For an explanation of Gaussian elimination, see Solve a system of equations with Gaussian elimination in C#. The following code shows how the example program finds polynomial least squares coefficients.
// Find the least squares linear fit. public static List<double> FindPolynomialLeastSquaresFit( List<PointF> points, int degree) { // Allocate space for (degree + 1) equations with // (degree + 2) terms each (including the constant term). double[,] coeffs = new double[degree + 1, degree + 2]; // Calculate the coefficients for the equations. for (int j = 0; j <= degree; j++) { // Calculate the coefficients for the jth equation. // Calculate the constant term for this equation. coeffs[j, degree + 1] = 0; foreach (PointF pt in points) { coeffs[j, degree + 1] -= Math.Pow(pt.X, j) * pt.Y; } // Calculate the other coefficients. for (int a_sub = 0; a_sub <= degree; a_sub++) { // Calculate the dth coefficient. coeffs[j, a_sub] = 0; foreach (PointF pt in points) { coeffs[j, a_sub] -= Math.Pow(pt.X, a_sub + j); } } } // Solve the equations. double[] answer = GaussianElimination(coeffs); // Return the result converted into a List<double>. return answer.ToList<double>(); }
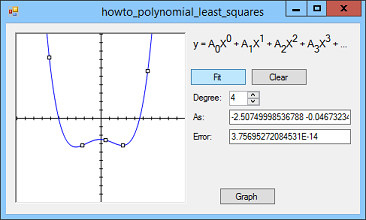
Give the program a try. It's pretty cool! Tip: Use the smallest degree that makes sense for your problem. If you use a very high degree, the curve will fit the points very closely but it will probably emphasize structure that isn't really there. For example, the previous picture on the right fits a degree 4 polynomial to points that really should be fit with a degree 2 polynomial. Download the example to experiment with it and to see additional details. |
![[Beginning Software Engineering, Second Edition]](book_sw_eng2_79x100.png)
![[Essential Algorithms, Second Edition]](book_algs2e_79x100.png)
![[The Modern C# Challenge]](book_csharp_challenge_80x100.jpg)
![[WPF 3d, Three-Dimensional Graphics with WPF and C#]](book_wpf3d_80x100.png)
![[The C# Helper Top 100]](book_top100_80x100.png)
![[Interview Puzzles Dissected]](book_interview_puzzles_80x100.png)
![[C# 24-Hour Trainer]](book_csharp24hr_2e_79x100.jpg)
![[C# 5.0 Programmer's Reference]](book_csharp_prog_ref_80x100.png)
![[MCSD Certification Toolkit (Exam 70-483): Programming in C#]](book_c_cert_80x100.jpg)
![Sum[(yi - (A0 * x^0 + A1 * x^1 + A2 * x^2 + ... + Ad*x^d)^2]](howto_polynomial_least_squares_eq1.png)
![Sum[(Ei)^2]](howto_polynomial_least_squares_eq2.png)
![Sum[2 * Ei * partial(Ei, Ak)]](howto_polynomial_least_squares_eq3.png)
![Sum[2 * Ei * (-xi^k)]](howto_polynomial_least_squares_eq4.png)
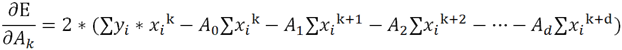
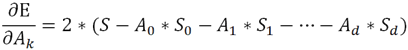
 The code simply builds an array holding the coefficients (the Ss in the previous equation) and then calls the
The code simply builds an array holding the coefficients (the Ss in the previous equation) and then calls the