Title: Use Gaussian elimination to solve a system of equations in C#

This example shows how to use Gaussian elimination to solve a linear system of equations of the form:

A1*x1 + B1*x2 + ... + N1*xn = C1 A2*x1 + B2*x2 + ... + N2*xn = C2 ... An*x1 + Bn*x2 + ... + Nn*xn = Cn

For example:

9 * x1 + 4 * x2 = 7 4 * x1 + 3 * x2 = 8

The solution to these equations gives values for x1 and x2 that make both equations true. (In this example, you can verify that the values -1 and 4 work.)

You can represent these equations as a matrix multiplied by a vector of variables x1, x2, ..., xn, resulting in a vector of constants C1, C2, ..., Cn.

| A1 B1 ... N1 | | x1 | | C1 | | A2 B2 ... N2 | | x2 | | C2 | | ... | * |... | = |... | | An Bn ... Nn | | xn | | Cn |

The helper method LoadArray loads data from text boxes into an augmented matrix that includes a column holding the constants and a final column that will eventually hold the solution. The augmented array has the form:

| A1 B1 ... N1 C1 0 | | A2 B2 ... N2 C2 0 | | ... 0 | | Am Bm ... Nm Cm 0 |

The following code shows the LoadArray method.

// Load the augmented array. // Column num_cols holds the result values. // Column num_cols + 1 will hold the variables' // final values after backsolving. private double[,] LoadArray(out int num_rows, out int num_cols) { // Build the augmented matrix. string[] value_rows = txtValues.Text.Split( new string[] {"\r\n"}, StringSplitOptions.RemoveEmptyEntries); string[] coef_rows = txtCoefficients.Text.Split( new string[] { "\r\n" }, StringSplitOptions.RemoveEmptyEntries); string[] one_row = coef_rows[0].Split( new string[] { " " }, StringSplitOptions.RemoveEmptyEntries); num_rows = coef_rows.GetUpperBound(0) + 1; num_cols = one_row.GetUpperBound(0) + 1; double[,] arr = new double[num_rows, num_cols + 2]; for (int r = 0; r < num_rows; r++) { one_row = coef_rows[r].Split( new char[] {' '}, StringSplitOptions.RemoveEmptyEntries); for (int c = 0; c < num_cols; c++) { arr[r, c] = double.Parse(one_row[c]); } arr[r, num_cols] = double.Parse(value_rows[r]); } return arr; }

When you click the Solve button, the program uses row operations to zero out leading terms in every row except one. For example, to zero out the leading term in the second row, the program multiplies each entry in the first row by -A2 / A1 and adds the result to the second row. Multiplying A1 by -A2 / A1 gives -A2, which cancels out the value in the first column of row 2. The program makes similar substitutions to zero out the first element in the other rows.

Next the program uses row 2 to zero out the second column in rows 3 and later. It continues in this way until it can no longer zero out rows. Ideally at that point the final row has the form | 0 0 ... Kn Ln |. This represents the equation 0*x1 + 0*x2 + ... + Kn*xn = Ln so it is easy to solve for xn. In that case, xn = Ln / Kn. The program plugs that value into the second-to-last row to calculate x(n-1) and continues "backsolving" up the list until it has a value for every variable.

// Solve the system of equations. private void cmdSolve_Click(object sender, EventArgs e) { const double tiny = 0.00001; string txt = ""; // Build the augmented matrix. // The values num_rows and num_cols are the number of rows // and columns in the matrix, not the augmented matrix. int num_rows, num_cols; double[,] arr = LoadArray(out num_rows, out num_cols); double[,] orig_arr = LoadArray(out num_rows, out num_cols); // Display the initial arrays. PrintArray(arr); PrintArray(orig_arr); // Start solving. for (int r = 0; r < num_rows - 1; r++) { // Zero out all entries in column r after this row. // See if this row has a non-zero entry in column r. if (Math.Abs(arr[r, r]) < tiny) { // Too close to zero. Try to swap with a later row. for (int r2 = r + 1; r2 < num_rows; r2++) { if (Math.Abs(arr[r2, r]) > tiny) { // This row will work. Swap them. for (int c = 0; c <= num_cols; c++) { double tmp = arr[r, c]; arr[r, c] = arr[r2, c]; arr[r2, c] = tmp; } break; } } } // If this row has a non-zero entry in column r, use it. if (Math.Abs(arr[r, r]) > tiny) { // Zero out this column in later rows. for (int r2 = r + 1; r2 < num_rows; r2++) { double factor = -arr[r2, r] / arr[r, r]; for (int c = r; c <= num_cols; c++) { arr[r2, c] = arr[r2, c] + factor * arr[r, c]; } } } } // Display the upper-triangular array. PrintArray(arr); // See if we have a solution. if (arr[num_rows - 1, num_cols - 1] == 0) { // We have no solution. // See if all of the entries in this row are 0. bool all_zeros = true; for (int c = 0; c <= num_cols + 1; c++) { if (arr[num_rows - 1, c] != 0) { all_zeros = false; break; } } if (all_zeros) { txt = "The solution is not unique"; } else { txt = "There is no solution"; } } else { // Backsolve. for (int r = num_rows - 1; r >= 0; r--) { double tmp = arr[r, num_cols]; for (int r2 = r + 1; r2 < num_rows; r2++) { tmp -= arr[r, r2] * arr[r2, num_cols + 1]; } arr[r, num_cols + 1] = tmp / arr[r, r]; } // Display the results. txt = " Values:"; for (int r = 0; r < num_rows; r++) { txt += "\r\nx" + r.ToString() + " = " + arr[r, num_cols + 1].ToString(); } // Verify. txt += "\r\n Check:"; for (int r = 0; r < num_rows; r++) { double tmp = 0; for (int c = 0; c < num_cols; c++) { tmp += orig_arr[r, c] * arr[c, num_cols + 1]; } txt += "\r\n" + tmp.ToString(); } txt = txt.Substring("\r\n".Length + 1); } txtResults.Text = txt; }

There's one problem with this method. Suppose you are trying to zero out items in column K but the value in position [K, K] is 0. Then you can't divide by the value to zero out other entries in that column. In that case, you can swap this row with one of the following rows that has a non-zero entry in that column and continue.

If there is no row to swap with, there are two possibilities. First, if every remaining entry in the array is zero, then the previous rows are true no matter what values the the following variables have so there is an infinite number of solutions. For example, consider the equations 1 * x0 - 1 * x1 = 2 and 2 * x0 - 2 * x1 = 4. These equations are true if x0 = x1 no matter what value x0 and x1 have.

The second possibility if you cannot finish zeroing out columns is that the final rows contain non-zero entries. In that case there is no solution possible. For example, the equations x0 + x1 = 0 and x0 + x1 = 1 do not have a solution.

Here are some other equations you can try to test the program:

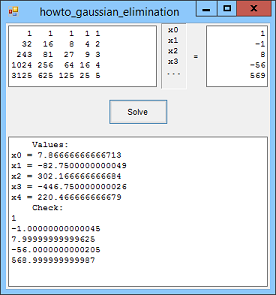
| 1 -3 1| |x1| | 4| | 2 -8 8| *|x2| = |-2| has solution 3, -1, -2. |-6 3 -15| |x3| | 9| | 9 3 4| |x1| | 7| | 4 3 4| *|x2| = | 8| has solution -0.2, 4, -0.8. | 1 1 1| |x3| | 3| | 1 1 1 1 1| |x1| | 1| | 32 16 8 4 2| |x2| | -1| | 243 81 27 9 3| * |x3| = | 8| |1024 256 64 16 4| |x4| |-56| |3125 625 125 25 5| |x5| |569| Has solution: x0 = 7.86666666666713 x1 = -82.7500000000049 x2 = 302.166666666684 x3 = -446.750000000026 x4 = 220.466666666679 | 2 -1 1| |x1| |1| | 3 2 -4| *|x2| = |4| has no solution. |-6 3 -3| |x3| |2| | 1 -1 2| |x1| |-3| | 4 4 -2| *|x2| = | 1| has no unique solution. |-2 2 -4| |x3| | 6|

For a more general and theoretical discussion on Gaussian elimination, see the article Gaussian Elimination by Eric W. Weisstein at MathWorld--A Wolfram Web Resource.

Download the example to experiment with it and to see additional details.