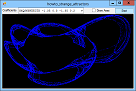
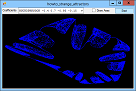
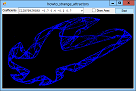
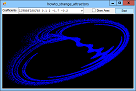
Title: Draw a variety of fractal strange attractors in C#

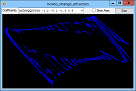
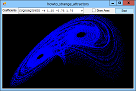
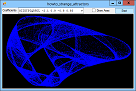
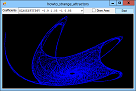
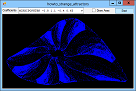
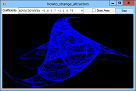
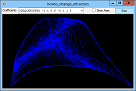
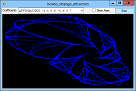
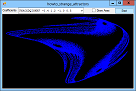
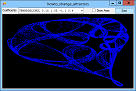
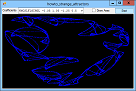
If you plot a sequence of points (x₁, y₁), (x₂, y₂), ..., the points can settle into one of several patterns. For example, they can converge on a fixed value, enter a repeating cycle, tend towards infinity, or look chaotic. They can also follow a strange attractor. In that case, the points clearly follow some pattern but not an obvious repeating cycle. This example plots points given by the equations:

X' = A0 + A1 * x + A2 * x2 + A3 * x * y + A4 * y + A5 * y2
Y' = A6 + A7 * x + A8 * x2 + A9 * x * y + A10 * y + A11 * y2

For various values of A₀, A₁, ... A₁₁. Different values of these coefficients produce different results.

The program uses a Timer to plot points so you can see the strange attractor growing. The following code shows the Tick event handler that draws the curve. It plots 1,000 points at a time to improve performance and to reduce flicker. For each iteration, the routine generates the next (X, Y) point and draws it on the Bitmap named m_Bitmap. After it has finished its 1,000 points, it refreshes picCanvas so you can see the result.

// Draw 1000 points. private double X, Y; private void tmrDrawPoint_Tick(object sender, EventArgs e) { for (int i = 1; i <= 1000; i++) { double new_x = A[0] + A[1] * X + A[2] * X * X + A[3] * X * Y + A[4] * Y + A[5] * Y * Y; double new_y = A[6] + A[7] * X + A[8] * X * X + A[9] * X * Y + A[10] * Y + A[11] * Y * Y; X = new_x; Y = new_y; int pix_x = (int)((X - Wxmin) / Wwid * m_Wid); int pix_y = (int)(m_Hgt - (Y - Wymin) / Whgt * m_Hgt - 1); if ((pix_x >= 0) && (pix_x < m_Wid) && (pix_y >= 0) && (pix_y < m_Hgt)) { Bm.SetPixel(pix_x, pix_y, Color.Blue); } } // Display the result. picCanvas.Refresh(); }

The calculations that convert X and Y into pix_x and pix_y translate and scale the points so they fill the bitmap nicely.

See the code for further details.

For more information on this kind of strange attractor, see the article Strange Attractor by Eric W. Weisstein at Wolfram MathWorld.

Download the example to experiment with it and to see additional details.