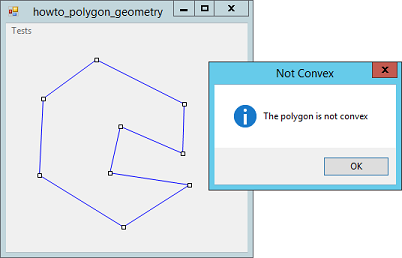
Title: Determine whether a polygon is convex in C#

To see if a polygon is convex, calculate the angles at each of the polygon's corners. If all of the angles have the same sign (either positive or negative depending on the orientation), then the polygon is convex.

Rather than actually finding the angles, you can just find the cross product of the segments on either side of the angles. If the segments at point B are AB and BC, then the cross product has value |AB| * |BC| * Sin(theta) where theta is the angle between the two segments. Because the lengths are always positive, the result is positive if the angle is positive and negative if the angle is negative.

The following code shows how this example's Polygon class determines whether a polygon is convex.

// Return True if the polygon is convex. public bool PolygonIsConvex() { // For each set of three adjacent points A, B, C, // find the cross product AB x BC. If the sign of // all the cross products is the same, the angles // are all positive or negative (depending on the // order in which we visit them) so the polygon // is convex. bool got_negative = false; bool got_positive = false; int num_points = Points.Length; int B, C; for (int A = 0; A < num_points; A++) { B = (A + 1) % num_points; C = (B + 1) % num_points; float cross_product = CrossProductLength( Points[A].X, Points[A].Y, Points[B].X, Points[B].Y, Points[C].X, Points[C].Y); if (cross_product < 0) { got_negative = true; } else if (cross_product > 0) { got_positive = true; } if (got_negative && got_positive) return false; } // If we got this far, the polygon is convex. return true; }

This method loops through the polygon's points. For each point A, it finds the indices of the preceding and following points A and C. It then uses the CrossProductLength method to calculate AB cross BC. The code keeps track of whether it has found positive or negative cross products. If it has found both, the method returns false to indicate that the polygon is not convex. If the code never finds both positive and negative cross products, it returns true to indicate that the polygon is convex.

The following code shows the CrossProductLength method.

// Return the cross product AB x BC. // The cross product is a vector perpendicular to AB // and BC having length |AB| * |BC| * Sin(theta) and // with direction given by the right-hand rule. // For two vectors in the X-Y plane, the result is a // vector with X and Y components 0 so the Z component // gives the vector's length and direction. public static float CrossProductLength(float Ax, float Ay, float Bx, float By, float Cx, float Cy) { // Get the vectors' coordinates. float BAx = Ax - Bx; float BAy = Ay - By; float BCx = Cx - Bx; float BCy = Cy - By; // Calculate the Z coordinate of the cross product. return (BAx * BCy - BAy * BCx); }

For more information on the cross product and how it is calculated, see Wikipedia and Wolfram MathWorld.

Note that the definition of convex for self-intersecting polygons is a bit fuzzy. If you interpret convex to mean that all angles have the same signs, then this example works just fine. That means, for example, that the star on the right is convex.

If you want convex to mean that the polygon has no "inner corners" like those the star has, then the method described here doesn't work for self-intersecting polygons. In that case, you should probably just check for self-intersection separately.

Download the example to experiment with it and to see additional details.