[Beginning Database Design Solutions, Second Edition]

Title: Draw a 3D Menger sponge fractal using WPF, XAML, and C#

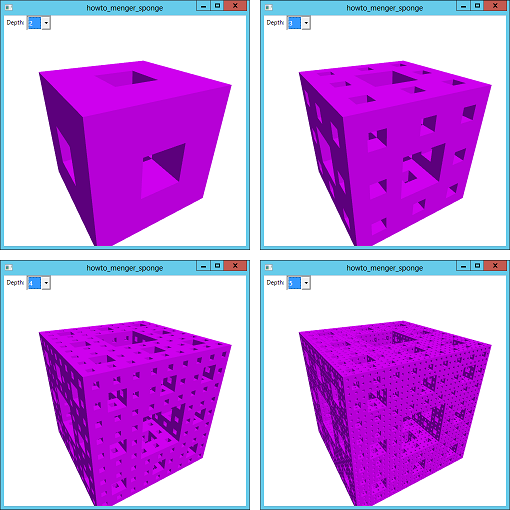
$Menger sponge fractal$

The algorithm for building a Menger sponge is simple in principle. Start with a cube. If you haven't yet reached the desired level of recursion, divide the cube into 27 sub-cubes and discard the 7 that don't touch any of the main cube's edges. Then recursively apply the method to the remaining 20 sub-cubes.

The following code shows the recursive MakeSponge method that this program uses.

// Make a Menger sponge. private void MakeSponge(MeshGeometry3D mesh, double xmin, double xmax, double ymin, double ymax, double zmin, double zmax, int depth) { // See if this is depth 1. if (depth == 1) { // Just make a cube. AddCube(mesh, xmin, xmax, ymin, ymax, zmin, zmax); } else { // Divide the cube. double dx = (xmax - xmin) / 3.0; double dy = (ymax - ymin) / 3.0; double dz = (zmax - zmin) / 3.0; for (int ix = 0; ix < 3; ix++) { for (int iy = 0; iy < 3; iy++) { if ((ix == 1) && (iy == 1)) continue; for (int iz = 0; iz < 3; iz++) { if ((iz == 1) && ((ix == 1) || (iy == 1))) continue; MakeSponge(mesh, xmin + dx * ix, xmin + dx * (ix + 1), ymin + dy * iy, ymin + dy * (iy + 1), zmin + dz * iz, zmin + dz * (iz + 1), depth - 1); } } } } }

If the remaining depth of recursion is 1, the method calls AddCube to draw the current cube, and the method is done. (The AddCube method simply adds 6 rectangles to make a cube. It's straightforward so it isn't shown here. Download the example to see how it works.)

If the remaining depth of recursion is greater than 1, the method calculates the dimensions of the cube's 27 sub-cubes. It loops through the possible cubes and calls itself recursively for those that aren't in the middle of the sub-cubes in the X, Y, or Z direction.

That's all there is to it. Like many recursive fractals, the code is remarkably short. It's also not too confusing (although that's not true of all short programs that draw fractals).

A much harder question is whether there is an easy way to not draw faces of cubes that lie inside the fractal. For example, if two cubes sit side-by-side, then you don't need to draw their common face because it is buried inside the solid. These fractals contain a LOT of faces, so the potential savings could be significant.

For more information on Menger sponges, see:

My book Essential Algorithms: A Practical Approach to Computer Algorithms describes a lot of other interesting algorithms including some two-dimensional recursive algorithms. For more information including a table of contents, go to the book's Wiley web page.

Download the example to experiment with it and to see additional details.