Title: Draw a star with a given number of points in C#

My goal here was to draw a "normal" star where the interior concave angles were located at intersections of lines connecting the exterior convex points. This turned out to be a more interesting problem than I expected. There's only one way to connect 5 or 6 points to make a star but for 7 or more points there are multiple ways to make a star. For example, the second picture (displayed below) shows two 7-pointed stars.

For a discussion of star polygons that includes an interesting chart showing the stars that are possible for different numbers of points, see the Wikipedia article Star polygon.

This program takes the number of points the star should have and the number of points that the program should skip when drawing the star. In the left star in the second figure, this skip number is 2 so the line leaving point 0 goes towards point 2 as indicated by the dashed line. In the star on the right the skip number is 3 so the line leaving point 0 heads towards point 3.
The DrawStar method shown in the following code draws the required star.

// Draw the indicated star in the rectangle. private void DrawStar(Graphics gr, Pen the_pen, Brush the_brush, int num_points, int skip, Rectangle rect) { // Get the star's points. PointF[] star_points = MakeStarPoints(-Math.PI / 2, num_points, skip, rect); // Draw the star. gr.FillPolygon(the_brush, star_points); gr.DrawPolygon(the_pen, star_points); }

The DrawStar method calls MakeStarPoints, passing it the angle at which the first point should be drawn, the number of points the star should have, the skip number, and the rectangle where the star should be drawn. It then fills and outlines the star. (The angle -Math.PI / 2 gives the point above the center of the star so the star is "right side up." You can change the start angle to rotate the star.)

The MakeStarPoints method shown in the following code does most of the interesting work.

// Generate the points for a star. private PointF[] MakeStarPoints(double start_theta, int num_points, int skip, Rectangle rect) { double theta, dtheta; PointF[] result; float rx = rect.Width / 2f; float ry = rect.Height / 2f; float cx = rect.X + rx; float cy = rect.Y + ry; // If this is a polygon, don't bother with concave points. if (skip == 1) { result = new PointF[num_points]; theta = start_theta; dtheta = 2 * Math.PI / num_points; for (int i = 0; i < num_points; i++) { result[i] = new PointF( (float)(cx + rx * Math.Cos(theta)), (float)(cy + ry * Math.Sin(theta))); theta += dtheta; } return result; } // Find the radius for the concave vertices. double concave_radius = CalculateConcaveRadius(num_points, skip); // Make the points. result = new PointF[2 * num_points]; theta = start_theta; dtheta = Math.PI / num_points; for (int i = 0; i < num_points; i++) { result[2 * i] = new PointF( (float)(cx + rx * Math.Cos(theta)), (float)(cy + ry * Math.Sin(theta))); theta += dtheta; result[2 * i + 1] = new PointF( (float)(cx + rx * Math.Cos(theta) * concave_radius), (float)(cy + ry * Math.Sin(theta) * concave_radius)); theta += dtheta; } return result; }

If the skip number is 1, the result is a regular polygon instead of a star, so the method doesn't need to allocate points for the star's concave points. In that case the method loops over the angles needed for each of the polygon's corners, creates a corresponding point, and returns the points.

If the skip number is greater than 1, the method calls the CalculateConcaveRadius method described next to see how far the star's concave points should be from the center. It then loops over the angles needed to create the star's convex and concave points, creates the points, and returns them. This loop is a bit more complicated than the previous one because it must generate convex points on the outside of the star and concave points on the inside of the star, but it's still reasonably easy to understand.

The following CalculateConcaveRadius method, which calculates the distance from the center of the star to the concave points, is a little more confusing.

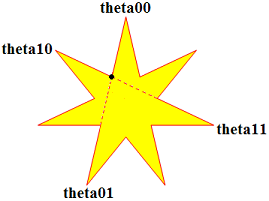
// Calculate the inner star radius. private double CalculateConcaveRadius(int num_points, int skip) { // For really small numbers of points. if (num_points < 5) return 0.33f; // Calculate angles to key points. double dtheta = 2 * Math.PI / num_points; double theta00 = -Math.PI / 2; double theta01 = theta00 + dtheta * skip; double theta10 = theta00 + dtheta; double theta11 = theta10 - dtheta * skip; // Find the key points. PointF pt00 = new PointF( (float)Math.Cos(theta00), (float)Math.Sin(theta00)); PointF pt01 = new PointF( (float)Math.Cos(theta01), (float)Math.Sin(theta01)); PointF pt10 = new PointF( (float)Math.Cos(theta10), (float)Math.Sin(theta10)); PointF pt11 = new PointF( (float)Math.Cos(theta11), (float)Math.Sin(theta11)); // See where the segments connecting the points intersect. bool lines_intersect, segments_intersect; PointF intersection, close_p1, close_p2; FindIntersection(pt00, pt01, pt10, pt11, out lines_intersect, out segments_intersect, out intersection, out close_p1, out close_p2); // Calculate the distance between the // point of intersection and the center. return Math.Sqrt( intersection.X * intersection.X + intersection.Y * intersection.Y); }

This method finds two line segments that intersect at one of the star's concave points. The first point is at the angle theta00. The star connects that point to the one at angle theta01 = theta00 + dtheta * skip. The star point next to the one at angle theta00 has angle theta10 = theta00 + dtheta. The star connects that point to the one at angle theta11 = theta01 - dtheta * skip. The figure on the right shows the situation.

After it finds these four angles, the method calculates the corresponding points pt00, pt01, pt10, and pt11. It then calls the FindIntersection method to see where the two line segments p00 --> p01 and p10 --> p11 intersect. For information on that method, see Determine where two lines intersect in C#.

Finally the CalculateConcaveRadius method calculates the distance from the point of intersection to the center of the star and uses that as the radius for the concave points.

Download the example to experiment with it and to see additional details.