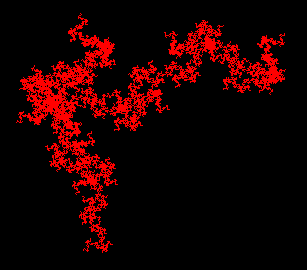
Title: Draw a curlicue fractal in C#

For information about how this fractal works, see Curlicue Fractal by Eric W. Weisstein from MathWorld, a Wolfram Web Resource.

The program starts by drawing a line segment in the direction of the X axis. It then iteratively calculates theta and phi using these equations:

theta(n + 1) = (theta(n) + 2 × Pi × S) mod (2 × Pi) phi(n + 1) = (theta(n) + phi(n)) mod (2 × Pi)

For some irrational number S. At each step, the program draws a new line segment in the direction given by phi.

The following DrawCurlicue method draws 10,000 segments following these rules.

// Draw the curve. private void DrawCurlicue(Graphics gr) { const int scale = 2; gr.ScaleTransform( scale, scale, MatrixOrder.Append); gr.TranslateTransform( picCanvas.ClientSize.Width / 2, picCanvas.ClientSize.Width / 2, MatrixOrder.Append); double s = double.Parse(txtS.Text); double theta, phi, x0, y0, x1, y1; theta = 0; phi = 0; x0 = 0; y0 = 0; // Use a zero-width pen so it draws as thin as possible // even after scaling. using (Pen thin_pen = new Pen(Color.Red, 0)) { for (int i = 1; i <= 10000; i++) { x1 = x0 + Math.Cos(phi); y1 = y0 + Math.Sin(phi); gr.DrawLine(thin_pen, (float)x0, (float)-y0, (float)x1, (float)-y1); x0 = x1; y0 = y1; phi = (theta + phi) % (2 * Math.PI); theta = (theta + 2 * Math.PI * s) % (2 * Math.PI); } } }

Download the example to experiment with it and to see additional details.