Title: Use a cryptographic random number generator in C#

The Random class generates random numbers, but they aren't cryptographically secure.

What does "cryptographically secure" mean? It means that an attacker, after seeing a series of random numbers that you generate, cannot predict the next one with any success.

This example uses a RNGCryptoServiceProvider to generate random numbers. (RNG stands for Random Number Generator.) The following code shows the RandomInteger method that generates random integers between an upper and lower bound.

// The random number provider. private RNGCryptoServiceProvider Rand = new RNGCryptoServiceProvider(); // Return a random integer between a min and max value. private int RandomInteger(int min, int max) { uint scale = uint.MaxValue; while (scale == uint.MaxValue) { // Get four random bytes. byte[] four_bytes = new byte[4]; Rand.GetBytes(four_bytes); // Convert that into an uint. scale = BitConverter.ToUInt32(four_bytes, 0); } // Add min to the scaled difference between max and min. return (int)(min + (max - min) * (scale / (double)uint.MaxValue)); }

At the class level, the program creates the RNGCryptoServiceProvider. The RandomInteger method uses that object to generate random numbers.

All the RNGCryptoServiceProvider does is generate bytes. It's up to you to convert those bytes into whatever values you need.

The RandomInteger method starts by setting the value scale to uint.MaxValue. I don't want the method to use that value for scale (you'll see why in a moment) so the method enters a while loop that executes as long as scale is uint.MaxValue.

Inside the loop, the method uses the RNGCryptoServiceProvider to generate four bytes. It then uses BitConverter.ToUInt32 to convert those four bytes into a four-byte unsigned integer (int) and sets scale equal to that value. If the bytes span all of the possible byte values (and they should), then the unsigned integer spans all possible unsigned integer values.

If scale is still uint.MaxValue, then the loop repeats until it gets a new value. (It is extremely unlikely that scale will be uint.MaxValue and much less likely that this will happen twice in a row so the loop won't last long.)

The code then divides scale by the uint.MaxValue. This produces a value between 0.0 and 1.0, not including 1.0. (This is why I didn't want scale to be uint.MaxValue--so the result of this division would be less than 1.0.) It multiplies this value by the difference between the maximum and minimum desired values and adds the result to the minimum value.

The final result is a value between min and max, not including max. The code then uses the (int) cast operator to truncate the result to get an integer. This matches the behavior provided by the Random class's Next method. It returns an integer between a lower bound (inclusive) and an upper bound (exclusive).

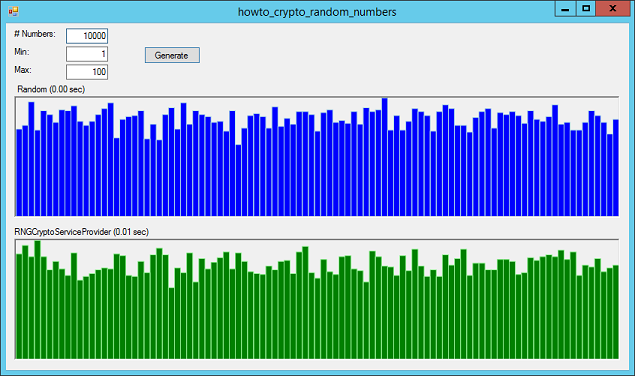
When you fill in the values and click Generate, the program generates random numbers and displays histograms showing their distribution. The more numbers you generate, the closer the histograms' bars should be to the same height.

First the program uses the Random class to generate random numbers and displays their histogram in the top PictureBox. Then it uses the RandomInteger method to generate a new set of numbers and displays their histogram in the bottom PictureBox. Looking at the histograms, both seem pretty "random."

Using a cryptographic random number generators has advantages and disadvantages.

• + It generates a different sequence even if you initialize it twice in rapid succession. If you do this with two Random objects, they are both initialized to the current time. If you do it quickly enough, they'll generate the same sequence of numbers. In fact, if you do this to quickly generate several random numbers, they may all be the same. (You can avoid this by only creating 1 Random object and reusing it each time you need a new number.)
• + An attacker cannot guess your random numbers. (Note that this isn't necessary for most programs.)
• - It's slow. In one test generating 10 million numbers, the Random class finished in 0.25 seconds but the RNGCryptoServiceProvider took 3.68 seconds, almost 15 times as long.
• - It's not repeatable. Sometimes it's useful to generate the same "random" sequence of numbers repeatedly so you can test a program. You can't do that with a cryptographic random number generator.

Later posts will use this method to easily generate cryptographically secure random numbers.

Download the example to experiment with it and to see additional details.