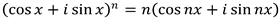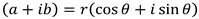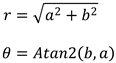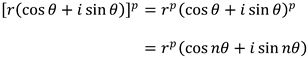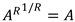Title: Add exponents to the complex number class in C#

This example uses only a little math (because I won't try to explain it), but if you really don't want the math, skip down to the Code section below.

Math

This example adds an exponentiation method to the complex number class described by the example Add square roots to the complex number class in C#.

De Moivre's formula (aka Moivre's theorem aka Moivre's identity) says that for any real number x and integer n:

This is useful because you can represent a complex number using polar coordinates like this:

Where:

That means we can use de Moivre's formula to calculate the nth power of the complex number like this:

For more information about de Moivre's formula, see the Wikipedia article De Moivre's formula.

Code

The Complex class uses the following ToPolar method to convert the complex number (which is stored with real part Re and imaginary par Im) into polar coordinates.

// Return the polar version of the number. public void ToPolar(out double r, out double theta) { r = Math.Sqrt(Re * Re + Im * Im); theta = Math.Atan2(Im, Re); }

The class defines the following method to return the number raised to a power.

// Use De Moivre's formula to raise the number to a power. public Complex Pow(double power) { // Get the polar representation. double r, theta; ToPolar(out r, out theta); // Use De Moivre's equation. double r_to_power = Math.Pow(r, power); double new_re = r_to_power * Math.Cos(power * theta); double new_im = r_to_power * Math.Sin(power * theta); return new Complex(new_re, new_im); }

This method uses the ToPolar method to convert the number into polar coordiates. It then uses de Moivre's formula to raise the number to the desired power and returns the result.

The main program uses the following code to test this method.

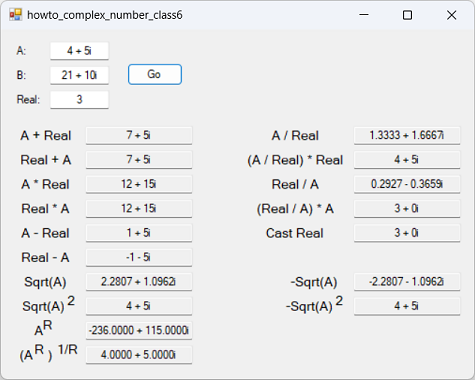
Complex a_to_r = A.Pow(R); txtAtoR.Text = a_to_r.ToString("0.0000"); Complex a_to_r_to_inverse = a_to_r.Pow(1.0 / R); txtAtoRtoInverse.Text = a_to_r_to_inverse.ToString("0.0000");

First the code calculates the complex number A raised to the power R and displays the result. It then raises that result to the power 1/R and displays that result. If it works, then:

So the final result should be the same as A. If you look at the picture at the top of the post, you'll see that this was true.

Download the example to experiment with it and to see additional details.