Title: Make a complex number class with overloaded operators in C#

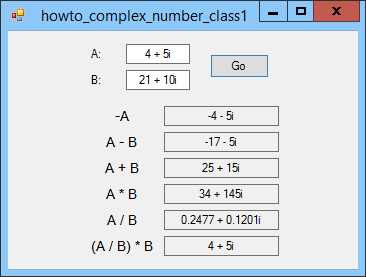
This example uses a complex number class to demonstrate operator overloading, a technique that allows you to define operators such as + and * for objects. Many people use a complex number class as an example because the operators are relatively easy to understand for complex numbers.

This example's Complex class has two public fields Re and Im to hold a complex number's real and imaginary parts.

class Complex { public double Re = 0, Im = 0; ... }

The class has a fairly obvious constructor that initializes the fields.

// Constructor using real and imaginary parts. public Complex(double real, double imaginary) { Re = real; Im = imaginary; }

Because a real number is also a valid complex number (for example, 7 = 7 + 0i), the class also has a constructor that takes a single real number as a parameter.

// Constructor using only a real part. public Complex(double real) : this(real, 0) { }

The syntax : this(real, 0) means C# should invoke some other constructor for the class passing it the parameters real and 0. That lets you use the more general constructor to implement this one without writing any new code.

So far, we just have code to initialize Complex objects. Now we need to overload operators such as + and * so they can work with Complex objects. The following code shows how the class defines the + operator to add two Complex objects.

// Return A + B. public static Complex operator +(Complex A, Complex B ) { return new Complex(A.Re + B.Re, A.Im + B.Im); }

Operator overloads must be static. The first Complex means this operation returns a Complex. That makes sense because a complex number plus another complex number gives you a new complex number.

After the keyword operator comes before the operator we are overloading, in this case +.

The parameters give the variables on which the operator will act. For example, suppose you have the following code.

Complex A = new Complex(1, 2); Complex B = new Complex(3, 4); Complex C = A + B;

In that case, when the code executes A + B, the parameters received by the operator's method are the Complex objects A and B. (I often name the first parameter me so I can think of it as the operand that is being operated upon.)

The body of the method simply adds the real and imaginary parts of the two parameters and uses the results to return a new Complex object.

Once you understand the syntax, the rest is fairly simple. The following code defines the unary - operator (so you can calculate -A).

// Return -A. public static Complex operator -(Complex A) { return new Complex(-A.Re, -A.Im); }

Note that defining the unary - operator (so you can calculate -A) does not automatically define a binary - operator (so you can calculate A - B). You need to define that operator separately. The following code defines the binary - and * operators.

// Return A - B. public static Complex operator -(Complex A, Complex B ) { return A + (-B); } // Return A * B. public static Complex operator *(Complex A, Complex B ) { return new Complex( A.Re * B.Re - A.Im * B.Im, A.Re * B.Im + A.Im * B.Re); }

Notice that the binary - operator uses the unary - operator and the + operator.

The only tricky operator defined by this example is /.

// Return A / B. public static Complex operator /(Complex A, Complex B ) { Complex conjugate = new Complex(B.Re, -B.Im); B *= conjugate; Complex numerator = A * conjugate; return new Complex( numerator.Re / B.Re, numerator.Im / B.Re); }

For an explanation of how this works, see for example this Khan Academy article Dividing complex numbers review.

Notice that the / operator's code uses the *= operator. If you overload an operator such as *, C# automatically defines the corresponding assignment operator, in this case *=.

This example also defines:

• A static Parse method that lets you easily parse text values to convert them into Complex objects much as int.Parse and double.Parse do.
• A ToString override that displays a Complex nicely formatted as in 3 + 9i.
• An overloaded ToString method that lets you pass a format string so you can format the real and imaginary parts as in 1.32 + 13.48i.

Those parts of the program are reasonably straightforward, so they aren't described here. See the code for details.

(The next example will continue developing the Complex class so stay tuned...)

Download the example to experiment with it and to see additional details.