
Title: Determine where two circles intersect in C#

This example shows one method for finding where two circles intersect in C#. If you don't like math, skip to the code below.
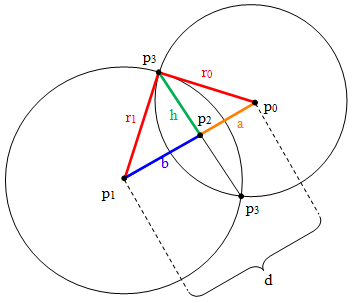 Consider the figure on the right showing two circles with radii r0 and r1. The points p0, p1, p2, and p3 have coordinates (x0, y0) and so forth.
Consider the figure on the right showing two circles with radii r0 and r1. The points p0, p1, p2, and p3 have coordinates (x0, y0) and so forth.
Let d = the distance between the circles' centers so 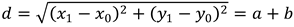 . Solving for a gives . Solving for a gives 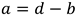 .Now there are three cases: .Now there are three cases:
- If d > r0 + r1: The circles are too far apart to intersect.
- If d < |r0 - r1|: One circle is inside the other so there is no intersection.
- If d = 0 and r0 = r1: The circles are the same.
- If d = r0 + r1: The circles touch at a single point.
- Otherwise: The circles touch at two points.
The Pythagorean theorem gives:
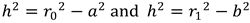
So:
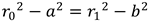
Substituting 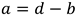 and multiplying this out gives: and multiplying this out gives:
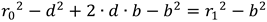
The -b2 terms on each side cancel out. You can then solve for b to get:
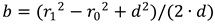
Similarly:
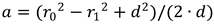
All of these values are known so you can solve for a and b. All that remains is using those distances to find the points p3.
If a line points in direction <dx, dy>, then two perpendicular lines point in the directions <dy, -dx> and <-dy, dx>. Scaling the result gives the following coordinates for the points p3:
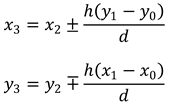
Be careful to notice the ± and ∓ symbols.
The Code
The following code shows the FindCircleCircleIntersections method that the program uses to find intersections.
// Find the points where the two circles intersect.
private int FindCircleCircleIntersections(
float cx0, float cy0, float radius0,
float cx1, float cy1, float radius1,
out PointF intersection1, out PointF intersection2)
{
// Find the distance between the centers.
float dx = cx0 - cx1;
float dy = cy0 - cy1;
double dist = Math.Sqrt(dx * dx + dy * dy);
// See how many solutions there are.
if (dist > radius0 + radius1)
{
// No solutions, the circles are too far apart.
intersection1 = new PointF(float.NaN, float.NaN);
intersection2 = new PointF(float.NaN, float.NaN);
return 0;
}
else if (dist < Math.Abs(radius0 - radius1))
{
// No solutions, one circle contains the other.
intersection1 = new PointF(float.NaN, float.NaN);
intersection2 = new PointF(float.NaN, float.NaN);
return 0;
}
else if ((dist == 0) && (radius0 == radius1))
{
// No solutions, the circles coincide.
intersection1 = new PointF(float.NaN, float.NaN);
intersection2 = new PointF(float.NaN, float.NaN);
return 0;
}
else
{
// Find a and h.
double a = (radius0 * radius0 -
radius1 * radius1 + dist * dist) / (2 * dist);
double h = Math.Sqrt(radius0 * radius0 - a * a);
// Find P2.
double cx2 = cx0 + a * (cx1 - cx0) / dist;
double cy2 = cy0 + a * (cy1 - cy0) / dist;
// Get the points P3.
intersection1 = new PointF(
(float)(cx2 + h * (cy1 - cy0) / dist),
(float)(cy2 - h * (cx1 - cx0) / dist));
intersection2 = new PointF(
(float)(cx2 - h * (cy1 - cy0) / dist),
(float)(cy2 + h * (cx1 - cx0) / dist));
// See if we have 1 or 2 solutions.
if (dist == radius0 + radius1) return 1;
return 2;
}
}
This code follows the explanation above.
Download the example to see additional details. When you click and drag twice to define two circles, the program uses the FindCircleCircleIntersections method to find their points of intersection (if any). It then draws the circles and the intersections.
Download the example to experiment with it and to see additional details.
|
![[C# Helper]](../banner260x75.png)

![[Beginning Database Design Solutions, Second Edition]](db2_79x100.png)
![[Beginning Database Design Solutions, Second Edition]](db2_79x100.png)