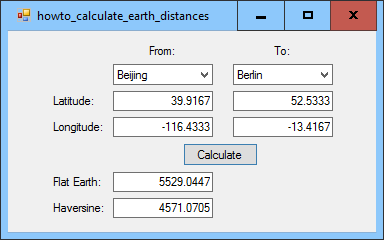
Title: Convert latitudes and longitudes into distances on the globe in C#

This example shows how you can convert latitudes and longitudes into distances on the globe. The formulas for performing those calculations is interesting but the program is also interesting for the ways it uses LINQ.

The program stores information about several important cities around the globe in CityData objects. The CityData class has Name, Latitude, and Longitude fields. The following code shows the class's most interesting method, a constructor that initializes an object from a string of the form "Delhi 28°40'N 77°14'E."

// Initialize with data of the form: "Delhi 28°40'N 77°14'E" // Data in this format is available at: // http://en.wikipedia.org/wiki/Latitude_and_longitude_of_cities public CityData(string data) { // Find the first digit. Regex reg_exp = new Regex(@"\d"); Match match = reg_exp.Match(data); int pos = match.Index; // Assign the name. Name = data.Substring(0, pos - 1).Trim(); // Parse the latitude. data = data.Substring(pos); pos = data.IndexOf('°'); double lat_degrees = double.Parse(data.Substring(0, pos)); data = data.Substring(pos + 1); pos = data.IndexOf('''); double lat_minutes = double.Parse(data.Substring(0, pos)); data = data.Substring(pos + 1); Latitude = lat_degrees + lat_minutes / 60; if (data.Substring(0, 1).ToUpper() == "S") Latitude = -Latitude; data = data.Substring(1).Trim(); // Parse the latitude. pos = data.IndexOf('°'); double long_degrees = double.Parse(data.Substring(0, pos)); data = data.Substring(pos + 1); pos = data.IndexOf('''); double long_minutes = double.Parse(data.Substring(0, pos)); data = data.Substring(pos + 1); Longitude = long_degrees + long_minutes / 60; if (data.Substring(0, 1).ToUpper() == "E") Longitude = -Longitude; }

This code simply parses the string to find the city's name, latitude, and longitude.

The main program uses the following code to initialize a series of cities.

// Locations of known cities. private CityData[] Cities = { new CityData("Rome 41°48 N 12°36'E"), new CityData("Tokyo 35°40 N 139°45'E"), new CityData("Mexico City 19°24 N 99°09'W"), ... new CityData("San Francisco 37°47 N 122°26'W"), };

The form's Load event handler uses the following code to make the form's two ComboBoxes display the city names.

// Load the list of cities. private void Form1_Load(object sender, EventArgs e) { var city_query = from CityData city_data in Cities orderby city_data.Name select city_data.Name; cboCityFrom.DataSource = city_query.ToArray(); cboCityTo.DataSource = city_query.ToArray(); cboCityTo.SelectedIndex = 1; }

This code uses LINQ to list the cities' names in sorted order. It then sets the DataSource properties of both ComboBox controls to the result of the query converted into an array. It finishes by selecting the cboCityTo control's second item (with index 1) so the two start with different cities selected.

When the user selects a city, the program copies the city's latitude and longitude into the corresponding TextBox controls. For example, the following code shows how the program gets information about the selected "To" city.

private void cboCityTo_SelectedIndexChanged( object sender, EventArgs e) { // Find the selected city. var city_query = from CityData city_data in Cities where (city_data.Name == cboCityTo.Text) select city_data; // Display the latitude and longitude. CityData city = city_query.First(); txtLatitudeTo.Text = city.Latitude.ToString("0.0000"); txtLongitudeTo.Text = city.Longitude.ToString("0.0000"); }

This code makes a LINQ query to select the CityData object with Name matching the selected city's name. It gets the first matching object and displays its latitude and longitude. The code that executes when the user selects a "From" city is similar.

After all that setup code, the program uses the following code to calculate the distance between the selected cities.

// Calculate the distances. private void btnCalculate_Click(object sender, EventArgs e) { // Get the entered latitudes and longitudes. double lat_from = double.Parse(txtLatitudeFrom.Text); if (lat_from < 0) lat_from += 360; double lon_from = double.Parse(txtLongitudeFrom.Text); if (lon_from < 0) lon_from += 360; double lat_to = double.Parse(txtLatitudeTo.Text); if (lat_to < 0) lat_to += 360; double lon_to = double.Parse(txtLongitudeTo.Text); if (lon_to < 0) lon_to += 360; // Calculate the differences in latitude and longitude. double dlat = Math.Abs(lat_from - lat_to); if (dlat > 180) dlat = 360 - dlat; double dlon = Math.Abs(lon_from - lon_to); if (dlon > 180) dlon = 360 - dlon; // Flat Earth. txtMethod1.Text = FlatEarth(lat_from, lon_from, lat_to, lon_to).ToString("0.0000"); // Haversine. txtMethod2.Text = Haversine(lat_from, lon_from, lat_to, lon_to).ToString("0.0000"); }

This code parses the latitudes and longitudes entered in the TextBox controls. It does a little processing to ensure that the latitudes and longitudes are between 0 and 360 degrees. It then calculates the differences in latitude and longitude and makes sure those are no greater than 180 degrees. (For example, a difference of 330 degrees is the same as a difference of 30 degrees in the other direction.)

Next the code invokes the FlatEarth and Haversine methods to calculate the actual distances. The following code shows the FlatEarth method.

// Methods for calculating distances. private const double EarthRadius = 3958.756; private double FlatEarth(double lat1, double lon1, double lat2, double lon2) { // Calculate the differences in latitude and longitude. double dlat = Math.Abs(lat1 - lat2); if (dlat > 180) dlat = 360 - dlat; double dlon = Math.Abs(lon1 - lon2); if (dlon > 180) dlon = 360 - dlon; double x = 69.1 * dlat; double y = 53.0 * dlon; return Math.Sqrt(x * x + y * y); }

This method is basically the Pythagorean theorem with the X and Y values adjusted by some reasonable scale factors. This method is only accurate for some parts of the globe.

The following code shows the Haversine method, which is more complicated but also more precise.

private double Haversine(double lat1, double lon1, double lat2, double lon2) { double dlat = DegreesToRadians(lat2 - lat1); double dlon = DegreesToRadians(lon2 - lon1); double a = Math.Sin(dlat / 2) * Math.Sin(dlat / 2) + Math.Cos(DegreesToRadians(lat1)) * Math.Cos(DegreesToRadians(lat2)) * Math.Sin(dlon / 2) * Math.Sin(dlon / 2); return 2 * Math.Atan2(Math.Sqrt(a), Math.Sqrt(1 - a)) * EarthRadius; } // Convert degrees into radians. private double DegreesToRadians(double degrees) { return degrees / 180 * Math.PI; }

The code converts the latitude and longitudes from degrees into radians and then uses the Haversine formula to calculate the distances. (For more information on the Haversine formula, see Wikipedia and Wolfram MathWorld.

Generally the Haversine method is closer to the correct distance than the FlatEarth method. Here are some sample values (in miles).