Title: Use "banker's rounding" and "normal rounding" in C#

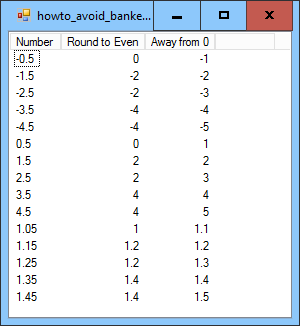
By default the Math.Round method uses "banker's rounding." In banker's rounding, a number that has a fractional part ending with a final digit of 5 is rounded to the nearest even number rather than to the next larger number as you might expect. The idea is that statistically half of a sample of numbers are rounded up and half are rounded down.

For example, if you want to round to the nearest tenth, the value 1.35 and 1.45 are both rounded to 1.4 because 4 is the closest even tenth.

In contrast if you use normal rounding, values are rounded away from 0. For example, 1.45 is rounded up to 1.5 and -1.45 is rounded down to -1.5.

Note that neither rule is needed if the number doesn't end with 5 in the final digit and that digit must be the one after the smallest digit that you want to keep. For example, suppose again that you're rounding to the nearest tenth. The value 1.4500001 is slightly bigger than 1.45 so it rounds up to 1.5 no matter which rounding scheme you're using.

The Math.Round method can take up to three parameters: the number to round, the number of digits after the decimal point to display, and a flag telling the method whether to use banker's rounding or to round away from 0.

The following code demonstrates using banker's rounding and normal rounding.

// By default, banker's rounding gives 1.4. double i = Math.Round(1.45, 1); // Rounding away from 0 gives 1.5. double j = Math.Round(1.45, 1, MidpointRounding.AwayFromZero);

The example program displays values for several numbers rounded with banker's rounding and normal "away from 0" rounding.

Download the example to experiment with it and to see additional details.